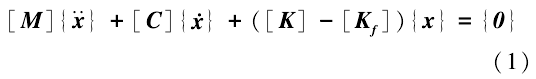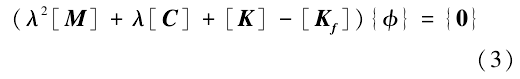摘要:目的 针对陶瓷人工髋关节置换术后患者出现的临床异响问题,探究异响产生的机制。方法 建立全骨盆-陶瓷人工髋关节假体-股骨系统的有限元模型,对其进行摩擦耦合下的复特征值分析,研究其在摩擦力作用下的动态响应;分析假体组件的振动特性,并通过对比组件和系统的模态振型,探究引起异响产生的振源。结果 随着摩擦系数的增加,假体系统发生了模态耦合,并产生了不稳定模态。不稳定模态振型主要表现为股骨组件的弯曲和扭转振动,同时在股骨组件的模态分析结果中存在频率与振型都与之相近的模态。另外,频率为1250Hz、2400Hz和3930Hz左右的不稳定模态具有较大的负模态阻尼比。股骨组件在不稳定模态频率1250Hz和2400Hz左右的弯曲共振和3930Hz左右的扭转共振是假体系统自激振动的振源。结论 模态耦合是摩擦引起假体系统自激振动的可能机制。骨盆也参与了噪声的辐射,同时也是假体系统产生不稳定模态的因素之一。
关键词:陶瓷髋关节;异响;骨盆;复特征值;自激励振动。
0引言
自1970年Boutin[1]首先将氧化铝陶瓷应用于全髋关节置换术后,陶瓷人工髋关节因其优越的摩擦学性能和良好的生物相容性已逐渐成为髋关节置换术的又一重要手段。然而,由于无法根本避免关节轴承面间摩擦的发生,陶瓷人工髋关节在临床使用中出现异响问题。异响现象不但对患者的心理状态造成负面影响,而且也反映了人工髋关节的摩擦磨损情况,成为陶瓷人工髋关节发展中的一个重要瓶颈[2-4].
临床研究表明,关节异响的发生概率为1%~10%[5-7],如此高的发生率,使得关节异响成为近年来医学与工学交叉研究的热点。Walter等[8]研究发现年轻、身高较高和体重较大的术后患者表现出更高的异响发生率,同时,发现髋臼在植入安装时,前倾角和外展角过大或过小都会导致边缘负重,增加异响的发生率。Nevelos[9]和Glaser[10]认为微分离现象会导致边缘负重,并形成条状磨损,使得局部区域的摩擦力增加,最终引起组件的振动。Restrepo等[4]研究了股骨柄的设计因素对关节异响的影响,结果表明使用的股骨柄刚度越小,患者的异响发生率越高。Pokorny[11]和Yang[12]认为金属髋臼设计不当会增加其边缘与股骨柄颈部的撞击,撞击产生的金属颗粒在关节面间形成三体磨损,破坏润滑,并产生异响。
一般认为异响的产生是由于假体系统在摩擦力的作用下产生了自激振动。Weiss等[13]通过复特征值法对关节异响问题进行了有限元分析,认为模态耦合可能是异响产生的机制。然而,其模拟预测的异响频率与实验测得的有所差异。Hothann[14]通过数值方法分析了假体部件的固有频率,发现陶瓷部件的固有频率远远大于人的听觉范围。Walter等[15]对产生异响的31对陶瓷配合面进行了声学采集,对比了假体各个部件的固有频率,也得到了相似的结果。这些结果使得一些学者认为异响的产生是源于金属部件的共振而非陶瓷部件。Currier等[16]建立了无金属部件的陶瓷髋关节假体模型,并在实验中复现了异响频率。华子恺等[17]建立了人工关节材料摩擦声学测试系统,分析了不同润滑形式下陶瓷关节材料的声学表现。目前,对异响产生机制的认识仍不明确,尤其对假体系统在摩擦力激励下的动态响应研究有待完善。
值得指出的是,在关节置换后,人工关节与人体骨骼肌肉形成了新的整体。对于陶瓷人工髋关节而言,其与骨盆、股骨以及肌肉韧带构成整体,重建了下肢支撑。其中,骨盆位于人体整个骨骼的中心位置,是人体躯干与下肢之间的连接部分,其结构复杂,能够传递重量并形成盆腔,但其是否对陶瓷人工髋关节因摩擦所造成的声学问题存在作用,需要深入探究。因此,对于陶瓷人工关节异响的研究而言,在现有关注摩擦界面的基础上,应当进一步开展整体性的研究。本文建立全骨盆-陶瓷髋关节假体-股骨的有限元模型,从摩擦自激振动出发,研究陶瓷关节的异响机制,并分析骨盆对异响的影响。
1研究方法与数值模型
1.1陶瓷关节异响的复特征值理论
复特征值分析法常用于制动噪声的分析,预测系统的不稳定模态[18].全骨盆-陶瓷人工髋关节假体-股骨系统的动力学方程可表示为:
式中:[M]、[C]和[K]别为系统的质量矩阵、阻尼矩阵和初始刚度矩阵,都是对称矩阵;{x}、{x}和{x}是节点的加速度矩阵、速度矩阵和位移矩阵;矩阵[Kf]是摩擦力耦合后的非对称刚度矩阵。由于摩擦耦合的存在,使假体系统的刚度矩阵由对称矩阵变为非对称矩阵,因此系统产生了复特征值,从而导致了不稳定模态的出现。
方程式(1)的通解形式为
带入式(1)得
式中:{φ}为特征向量,即模态振型,表示系统振动的变形形状;λ为系统的特征值,λ=α+iω。实部α反应了系统运动的稳定性,为正值时,表示系统处于不稳定状态;虚部ω为振动时的固有频率。模态分析中常用模态阻尼比[ζ=-α/(π丨ω丨)]来表示系统不稳定的趋势,ζ为负则系统不稳定。
1.2模型的建立及其组件材料
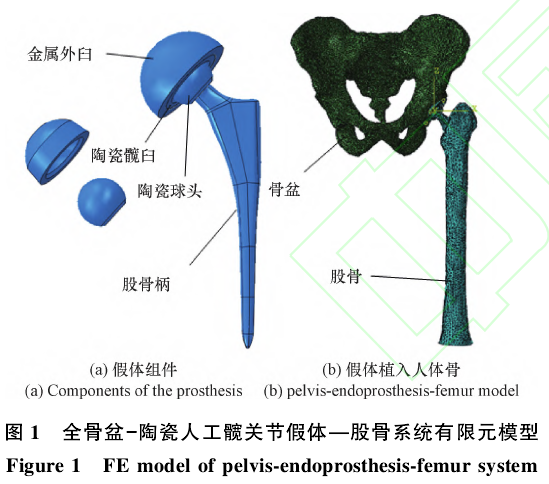
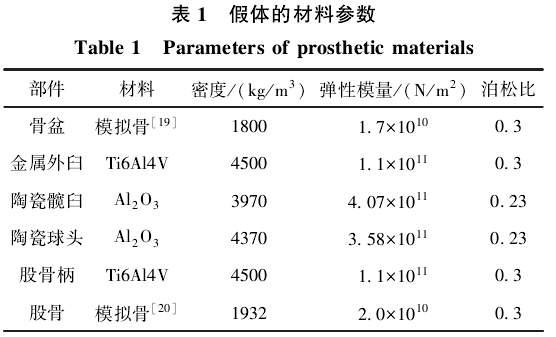
全骨盆-陶瓷人工髋关节假体-股骨系统模型如图1所示,包括金属外臼、陶瓷髋臼、陶瓷球头、股骨柄[图1(a)]以及完整的人体骨盆与股骨[图1(b)].其中骨盆和股骨模型来自志愿者的断层扫描CT数据,假体模型来自实际假体产品。骨盆、股骨在Mimics软件中完成三维重建并体网格化后,导入Abaqus软件中完成系统装配与分析。各部件的材料属性如表1所示。有限元网格[图1(b)]采用C3D4.由于陶瓷髋臼和陶瓷球头的摩擦副表面为主分析界面,因此对其进一步细化网格。
1.3假体系统的分析过程
全骨盆-陶瓷人工髋关节假体-股骨系统的模态分析包含以下4个分析步骤。
(1)带关节合力的非线性静态分析。
(2)考虑转速的非线性静态分析。
(3)不考虑阻尼情况下,系统的固有频率分析。
(4)考虑摩擦偶合效应的复特征值分析。
陶瓷髋臼和陶瓷球头表面形成相对运动,为主要分析界面,其切向接触属性定义为罚函数摩擦方程(摩擦系数取0.1~0.5)[21],选择有限滑移运算法则。金属外臼与陶瓷髋臼,股骨柄与陶瓷球头,假体与骨盆及股骨的接触为绑定约束。
研究表明关节合力是人体体重的2~3倍[14],假设成年人重60kg,则髋关节合力可以设为1500N[22].第(1)步将关节合力分解为均布载荷垂直于地面向上施加于股骨组件底部(如图2粉色箭头所示)。边界条件中将骶椎S1面节点设为全约束[23],并约束股骨远端边缘节点X、Y方向的位移自由度。第(2)步将陶瓷球头、股骨柄和股骨作为一个整体,施加绕X轴的转动,转速为1rad/s以模拟人体步态转速[20],此时关节轴承面将产生摩擦滑移,从而产生摩擦力。Abaqus复特征值分析使用的是子空间投影法,因此需要通过第(3)步进行正则模态分析,为复特征值的提取提供子空间模态。第(4)步复特征值分析后可得到系统的模态参数,并由此判断系统的稳定性以预测系统产生异响的趋势。
1.4假体组件的振动特性分析
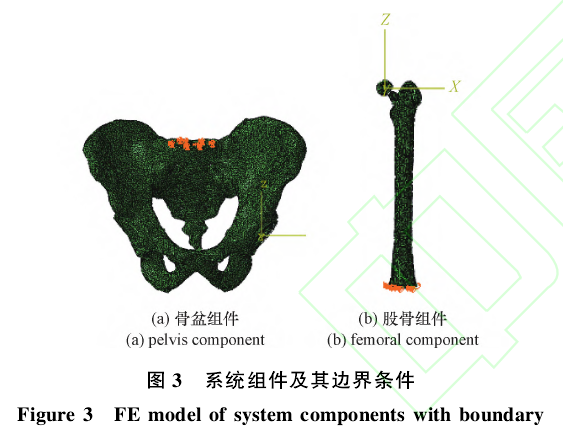
假体组件的振动特性包括组件的固有频率和固有振型。Walter[15]、Sariali[24]分析了单个部件的振动特性,认为金属部件的共振是异响发生的振源。然而,假体系统具有特定的结构和约束条件,必须进一步做整体性分析。在人工髋关节置换术中,金属外臼牢牢地固定在盆骨中,而陶瓷髋臼与金属外臼也是固定在一起的,所以骨盆、金属外臼和陶瓷髋臼可以作为一个整体来分析。陶瓷球头与股骨柄的颈部牢固的装配在一起,然后通过骨水泥将股骨柄固定在大腿骨中,所以陶瓷球头、股骨柄、股骨也可以作为一个整体来分析。将假体系统分为上述两个部分,分别命名为骨盆组件和股骨组件。对两个组件进行模态分析,以得到组件的振动特性,其中组件模态分析过程中的边界条件与假体系统分析过程中的边界条件保持一致(图3)。
2结果
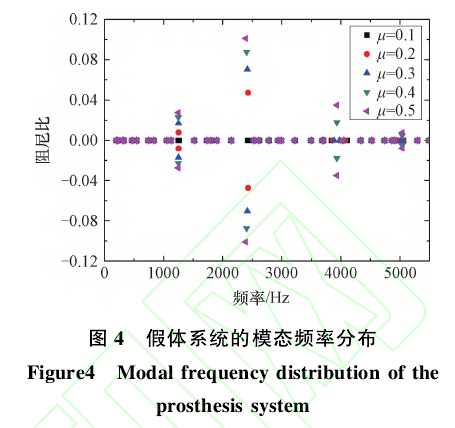
假体系统的不稳定模态频率与摩擦系数的关系如图4所示,其中X轴为系统的模态频率,Y轴为系统的模态阻尼比。由图4可知,随着摩擦系数的增加,不稳定的模态频率的数量增加,模态频率所对应的模态阻尼比的绝对值增大。当摩擦系数μ=0.1时,无不稳定模态频率,假体系统稳定。当摩擦系数μ=0.2时,不稳定模态频率为1254.3Hz、2429.6Hz,其对应的模态阻尼比为-0.00800、-0.04739.当摩擦系数μ=0.4时,假体系统的不稳定模态频率增加到4个,且频率在1250Hz和2400Hz左右的模态阻尼比分别增加到-0.02292、-0.08758.
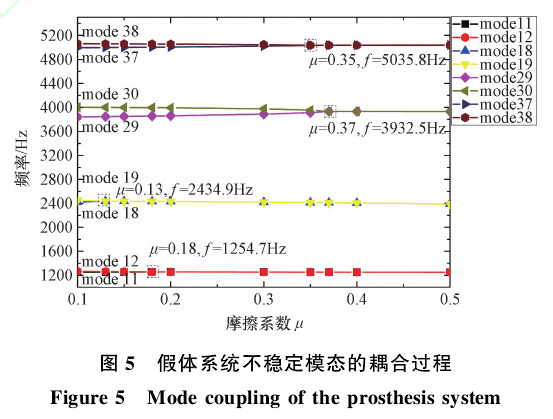
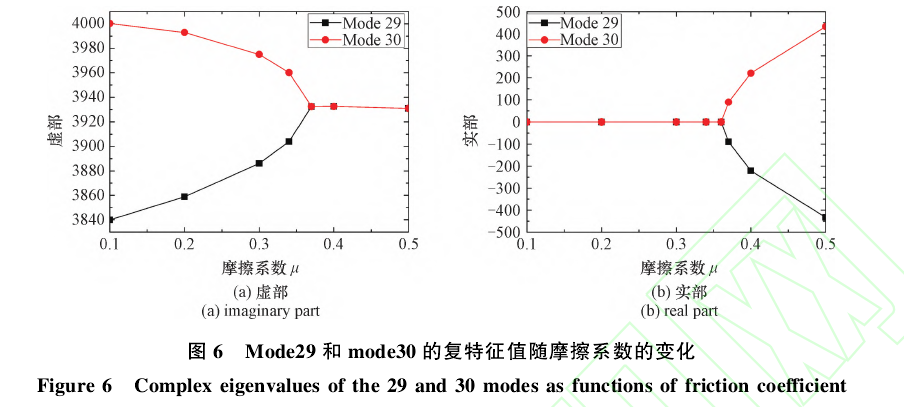
图5表示了模态频率随着摩擦系数变化的耦合过程,其中X轴为系统的摩擦系数,Y轴为随着摩擦系数的增加参与耦合的模态频率。随着摩擦系数的增加,一对相邻的模态频率相互靠近,当摩擦系数增加到大于某一临界摩擦系数时,两相邻模态频率完全重合,假体系统发生模态耦合,并引起假体系统的不稳定。如图6所示,mode29和mode30随着摩擦系数增加到μ=0.37时发生耦合,其特征值具有相同的虚部,而特征值实部成相反数相互远离。其中mode30特征值实部为正,为不稳定模态。
表2为摩擦系数μ=0.4时,假体系统在不稳定模态频率1250.3Hz、2404.7Hz、3932.6Hz和5037.0Hz时的模态振型及模态阻尼比。其中,股骨组件的变形较骨盆组件明显,表现为绕X、Y轴的弯曲振动,绕Z轴的扭转振动及陶瓷球头的大变形。当摩擦系数取其他值时,不稳定模态频率和振型相似,这里不再赘述。
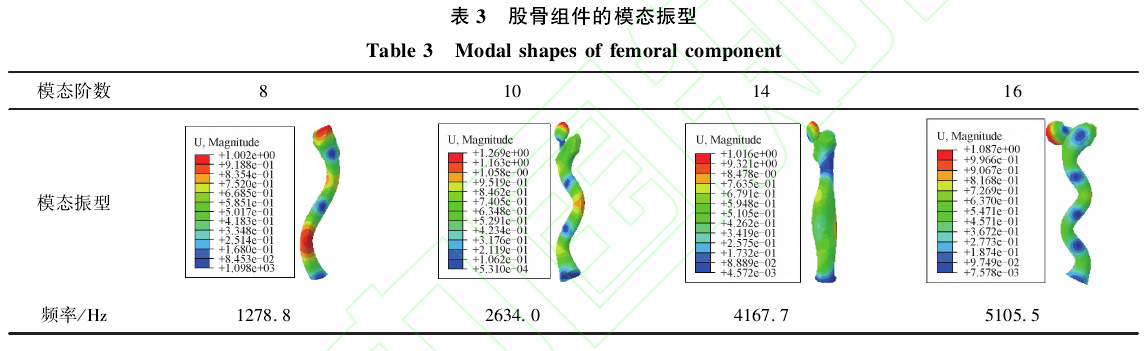
为了探究假体系统产生异响的振源,分析了6000Hz以内股骨组件和骨盆组件的振动特性。通过比较系统的不稳定模态振型,选取股骨组件和骨盆组件的模态振型列于表3和表4中。由表可知,虽然陶瓷髋臼和陶瓷球头的固有频率远大于人的听觉范围,然而在考虑其在假体系统中的结构和约束关系时,其振动频率接近异响频率[15-16].
3讨论
图4与图5的结果显示,系统的不稳定模态频率主要发生在1250Hz、2400Hz、3930Hz和5040Hz左右。Walter等[15]临床实际测得异响频率为1546Hz、3046Hz和4593Hz.Currier等[16]临床实际测得的异响频率为1540Hz、3090Hz和4620Hz.本次仿真预测到的异响频率与临床结果相吻合。这证明了全骨盆-陶瓷人工髋关节假体-股骨系统模型的准确性和使用复特征值法研究关节异响的可靠性。
摩擦系数制约着假体的稳定性,如图4所示,当摩擦系数μ=0.1时系统不存在不稳定模态。当摩擦系数μ=0.2时,系统有2个不稳定模态,当摩擦系数μ=0.4时,系统有4个不稳定模态,并且同一阶模态阻尼比的绝对值也随着摩擦系数的增加而增加。这说明,随着摩擦系数的增加,假体系统的不稳定性增强,异响越易发生。
图5、图6很好地解释了假体系统的摩擦自激振动过程。频率值接近的两相邻模态,随着摩擦系数的增加以相同的频率发生耦合,其中一个模态变得不稳定。如mode29和模态30在临界摩擦系数μ=0.37时发生耦合,其中mode30的特征值具有正实部,为不稳定模态。假体系统的异响现象可解释为在摩擦力的作用下,引起了两个相邻模态相互耦合,并导致了假体系统的自激振动。
从表2可以看出系统所有不稳定模态振型的主要变形都发生在股骨组件上,且在股骨组件的模态分析结果中能够找到与之相近的模态振型(表3)。例如,假体系统的第12阶模态不稳定,其频率和振型分别与表3中股骨组件的第8阶模态频率和振型相近,这说明股骨组件在摩擦力激励下的共振是异响产生的振源。
如表2所示,mode12和mode19的模态振型主要表现为股骨组件的弯曲变形和骨盆组件的微小变形。mode30的模态振型主要表现为股骨组件的扭转变形,同时骨盆组件具有明显的变形。值得注意的是,在mode38的模态振型中,最大的变形发生在骨盆的尾椎上。然而其模态阻尼比的绝对值远小于其他不稳定模态。且从能量角度而言,频率低的不稳定模态在实际情况中容易被激发出来[25].因为低频振动相对高频振动所需要的能量较少,系统产生的摩擦能量会先满足低频振动的需要,之后往往难以满足高频振动的需要。Mode12、mode19和mode30具有较小的频率和较大的模态阻尼比,进一步说明了股骨组件的弯曲共振和扭转共振是系统不稳定振动的振源,是异响产生的根本原因,这与Ehsan[26]的计算结果相符。
尽管异响的发生主要源于股骨组件的共振,然而骨盆作为重要的连接部分,其作用不能忽略。由表2可知,骨盆的振动也是假体系统不稳定模态振型的组成部分。对于mode30的振型而言,其骨盆变形与股骨组件的变形处于同一量级,并与表4中骨盆组件第19阶模态振型相似。这说明,骨盆参与了噪声的辐射,同时也是假体系统产生不稳定模态的因素之一。
4结论
本文针对陶瓷人工髋关节异响问题,建立了全骨盆-陶瓷人工髋关节假体-股骨系统的有限元模型,利用有限元模拟,进行了异响产生机制的探究,主要结论如下。
(1)本次模拟结果与临床实际测得的异响频率相吻合,验证了全骨盆-陶瓷人工髋关节假体-股骨系统模型的正确性。
(2)陶瓷人工髋关节异响的产生机制是在摩擦系数增加到大于某一临界摩擦系数时,系统两相邻模态相互耦合,并导致了股骨组件的弯曲或扭转共振。
(3)骨盆参与了噪声的辐射,同时也是假体系统产生不稳定模态的因素之一。
参考文献
[1]Boutin P. Total arthroplasty of the hip by fritted aluminumprosthesis:Experimental study and 1st clinical applications[J].Revue De Chirurgie Orthopedique Et Reparatrice De L AppareilMoteur,1972,58 (3):229-246.
[2]Keurentjes JC,Kuipers RM,Wever DJ,et al. High incidence ofsqueaking in THAs with alumina ceramic-on-ceramic bearings[J]. Clinical Orthopaedics & Related Research,2008,466(6):1438-1443.
[3]Walter WL,Yeung E,Esposito C. A review of squeaking hips[J].Journal of the American Academy of Orthopaedic Surgeons,2010,18(6):319-326.
[4]Restrepo C,Post ZD,Kai B,et al. The effect of stem design onthe prevalence of squeaking following ceramic-on-ceramic bearingtotal hip arthroplasty [J]. The Journal of Bone and Joint Surgery,2010,92(3):550-557.
[5]Capello WN, D' Antonio JA, Feinberg JR, et al. Ceramic-on-ceramic total hip arthroplasty: update [J ]. The Journal ofarthroplasty,2008,23(7):39-43.
[6]Jarrett CA,Ranawat AS,Bruzzone M,et al. The squeaking hip:aphenomenon of ceramic-on-ceramic total hip arthroplasty[J]. TheJournal of Bone & Joint Surgery,2009,91(6):1344-1349.
[7]Restrepo C,Parvizi J,Kurtz SM,et al. The noisy ceramic hip:iscomponent malpositioning the cause- [J ]. The Journal ofarthroplasty,2008,23(5):643-649.
[8]Walter WL,O'Toole GC,Walter WK,et al. Squeaking in ceramic-on-ceramic hips: The importance of acetabular componentorientation[J]. The Journal of arthroplasty,2007,22(4):496-503.
[9]Nevelos J, Ingham E, Doyle C, et al. Microseparation of thecenters of alumina-alumina artificial hip joints during simulatortesting produces clinically relevant wear rates and patterns[J].The Journal of Arthroplasty,2000,15(6):793-795.
[10]Glaser D,Komistek RD,Cates HE,et al. Clicking and squeaking:in vivo correlation of sound and separation for different bearingsurfaces[J]. The Journal of Bone & Joint Surgery, 2008,90(4):112-120.
[11]Pokorny A, Knahr K. The Squeaking Phenomenon in Ceramic-on-Ceramic Bearings[M] / / Tribology in Total Hip Arthroplasty.Springer Berlin Heidelberg,2011:99-109.
[12]Yang CC,Kim RH,Dennis DA. The squeaking hip a cause forconcern-disagrees[J]. Orthopedics,2007,30(9):739.
[13]Weiss C, Gdaniec P, Hoffmann NP, et al. Squeak in hipendoprosthesis systems: an experimental study and a numericaltechnique to analyze design variants[J]. Medical Engineering &Physics,2010,32(6):604-609.
[14]Hothann A,Weiss C, Hoffman N,et al. Squeaking ceramic-on-ceramic total hip replacements. A numerical vibration approach[C ]. Switzerland: 16th Congress of the European Society ofBiomechanics. Luzern,2008.
[15]Walter WL,Waters TS,Gillies M,et al. Squeaking hips [J]. TheJournal of Bone & Joint Surgery,2008,90(4):102-111.
[16]Currier JH, Anderson DE, Van Citters DW. A proposedmechanism for squeaking of ceramic-on-ceramic hips[J]. Wear,2010,269(11):782-789.
[17]华子恺,桑仁政,张建华。人工关节材料生物摩擦声学测试研究[J].机械工程学报,2012,48(3):128-132.Hua Zikai, Sang Renzheng, Zhang Jianhua. Biotribo-acousticstudy on artificial joint materials [J]. Journal of MechanicalEngineering,2012,48(3):128-132.
[18]陈光雄,戴焕云,曾京,等。踏面制动尖叫噪声的有限元分析[J].机械工程学报,2009,45(3):203-207.Chen Guangxiong,Dai Huanyun,Zeng Jing,et al. Finite elementanalysis of the squeal propensity for a pad-wheel tread brakesystem reduction[J]. Journal of Mechanical Engineering,2009,45(3):203-207.
[19]Phillips ATM, Pankaj P, Howie CR, et al. Finite elementmodelling of the pelvis: inclusion of muscular and ligamentousboundary conditions[J]. Medical Engineering and physics,2007,29(7):739-748.
[20]Fan N,Chen GX,Qian LM. Analysis of squeaking on ceramic hipendoprosthesis using the complex eigenvalue method[J]. Wear,2011,271(9):2305-2312.
[21]Sariali E,Stewart T,Jin Z,et al. In vitro investigation of frictionunder edge-loading conditions for ceramic-on-ceramic total hipprosthesis[J]. Journal of Orthopaedic Research,2010,28( 8):979-985.
[22]Bergmann G,Deuretzbacher G,Heller M,et al. Hip contact forcesand gait patterns from routine activities [J ]. Journal ofBiomechanics,2001,34(7):859-871.
[23]姬涛,郭卫,汤小东,等。组配式人工半骨盆假体在步行周期载荷下的有限元分析[J].北京大学学报:医学版,2010,42(2):192-196.Ji Tao,Guo Wei,Tang Xiaodong,et al. Finite element analysis formodular hemipelvic endoprosthesis during loaded gait cycle [J].Journal of Peking University:Health Sciences,2010,42(2):192-196.
[24]Sariali E,Stewart T,Jin Z,et al. Three-dimensional modeling of invitro hip kinematics under micro-separation regime for ceramic onceramic total hip prosthesis: an analysis of vibration and noise[J]. Journal of Biomechanics,2010 43(2):326-333.
[25]Nouby M,Mathivanan D,Srinivasan K. A combined approach ofcomplex eigenvalue analysis and design of experiments(DOE) tostudy disc brake squeal[J]. International Journal of Engineering,Science and Technology,2009,1(1):254-271.
[26]Askari E, Flores P, Dabirrahmani D, et al. Nonlinear vibrationand dynamics of ceramic on ceramic artificial hip joints:a spatialmultibody modelling [J]. Nonlinear Dynamics, 2014, 76 ( 2):1365-1377.