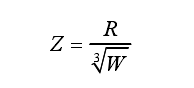利用超压准则确定爆炸荷载作用下的梁体是否破坏可得到偏安全的计算结果;随着炸药使用当量的增大、安放比例距离的减小,钢筋混凝土梁体损伤程度将变大;炸药放在梁体上方产生的损伤比放在梁下方严重;炸药放置位置越靠近梁体端部,钢筋混凝土梁越容易发生剪切损伤。
以下为本篇论文正文:
摘 要:针对爆炸荷载对桥梁的损伤,以市内轻轨交通常用的简支T梁为例,采用非线性显式动力学分析软件,对某钢筋混凝土T梁进行了爆炸作用下的损伤研究。讨论了炸药当量、炸药相对于梁的位置以及比例距离等参数对梁体损伤的影响。分析结果表明,减小比例距离、增大炸药当量和将炸药放置在接近梁端的上部这3种情况将加剧钢筋混凝土梁的损伤。
关键词:损伤分析;爆炸模拟;钢筋混凝土梁;比例距离;炸药当量
2015年8月12日晚,天津塘沽一危险品仓库发生了大爆炸,造成了极大的生命财产损失,也引发了恶劣的社会影响。津滨轻轨9号线位于爆炸影响范围内,受其影响部分轻轨桥梁出现了不同程度的破坏和损伤,见图1.
城市交通中桥梁作为重要的交通节点,发生爆炸势必造成极大的危害。发生爆炸后桥梁本身容易发生破坏,桥梁体积大质量重,发生坍塌将带来极大的经济损失,造成周围人员伤亡。所以在桥梁设计中充分考虑爆炸因素的影响是十分必要的也是极其紧迫的。城市交通中桥梁虽然处于城市,但也潜伏着很多爆炸隐患,其中大多数是人为因素,比如:桥梁内部一些老化的燃油、燃气管线引发爆炸,恐怖袭击等不可抗因素。
当前关于爆炸的研究已经很多,Rogers[1]、Baker等[2-3]对爆炸现象进行了理论研究,推导出了一些具有指导意义的经验公式;Krauthammer等[4-6]分析了脉冲荷载作用下以及瞬时荷载作用下钢筋混凝土板和梁的响应;方秦等[7-8]、张媛媛等[9]、焦延平等[10]、张秀华等[11]运用有限元软件对爆炸作用下的结构物损伤情况进行了相关的数值模拟分析。
目前,关于结构爆炸的研究存在以下不足:出于结构抗爆研究具有特殊性和复杂性的原因,大多数学者以结构构件为研究对象展开了大量的研究,而以结构整体作为研究对象加以研究的较少;对于爆炸荷载的简化存在不合理之处,通常以双直线形式荷载代替爆炸荷载,这种简化与实际情况存在较大差异;有限元分析中关于爆炸荷载的模拟存在不足,对于空气与结构之间的流、固耦合作用考虑不周也将降低模拟精度。针对现有研究的不足,本文以天津地铁典型简支T梁桥为例利用有限元分析软件建立了优化模型,模拟了爆炸发生时T梁的动力响应,对于梁结构的损伤进行了动力时程分析。文中以爆炸比例距离、炸药当量以及炸药相对于梁的位置等作为基本研究参数,分别分析了各参数对爆炸效应的影响情况。分析结果可以为类似桥梁工程的抗爆炸设计提供理论支撑,同时为桥梁结构在爆炸作用下的损伤研究提供一定的方法借鉴。
1分析模型与评价指标
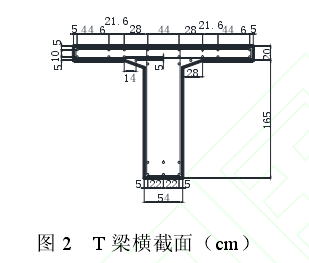
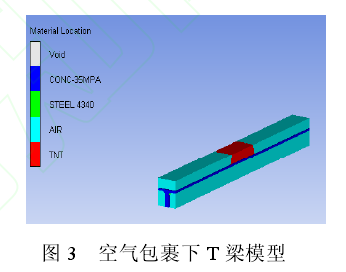
本文以典型简支T梁桥为例,建立有限元模型,开展爆炸损伤研究。T梁桥横截面形式及尺寸如图2所示,空气包裹下T梁模型见图3.
分析模型中T梁使用三维实体单元,钢筋使用梁单元加以模拟。建立模型时将炸药置于空气单元的局部区域内,钢筋单元与混凝土做耦合处理。模型中空气与混凝土的计算分别采用了Euler求解器和Lagrange求解器。定义边界条件时,在梁体一端形成固定支座,另一端形成可动铰支座。模型中空气单元包裹梁单元形成整体,空气域边界设定为Flow out (Euler)物质流出。在Lagrange方法中,炸药单元与空气单元之间通过公用节点方式建立联系,将炸药定义成流体以避免爆炸过程中网格的过分畸变对计算结果产生不利影响。炸药起爆后冲击波在自由场中传播,当冲击波将到达结构或界面时对混凝土T梁产生破坏作用。
一般情况下,对于梁体破坏的定义有3种理论,即第一强度准则、超压准则、最大挠度理论等。其中,第一强度准则认为应力波造成的结构破坏取决于应力值大小,主要发生的是拉伸破坏,以第一强度理论作为破坏准则[12].超压准则[13]指出爆炸波的超压只有达到某一临界数值时才能够对物体产生破坏作用。因此,爆炸波是否具有破坏能力直接取决于超压值的大小,其中比例距离下的超压临界值的确定在我国国防工程设计规范[14]中给出了计算方法。我国桥梁设计规范(JTG D 62-2004)中对于最大挠度理论给出了相应的规定。本文以梁体测试点的应力、超压值和挠度等作为主要指标,分析了比例距离、炸药当量以及炸药相对于梁的位置等参数对爆炸效应的影响。
2分析参数
根据既有文献,炸药当量、比例距离、炸药在梁上和梁下相同位置处以及炸药相对于梁上的不同跨径是爆炸对混凝土梁体结构造成破坏作用的主要影响因素,也是本文所确定的分析参数。作为测点的炸药垂直投影点是受爆炸荷载作用影响最大、破坏最为严重的点。模型分析中各参数的取值如表1所示,通过改变模型中各参数的取值,可以分析梁体测试点处的应力、超压值以及竖向位移等变化情况。
2.1炸药当量
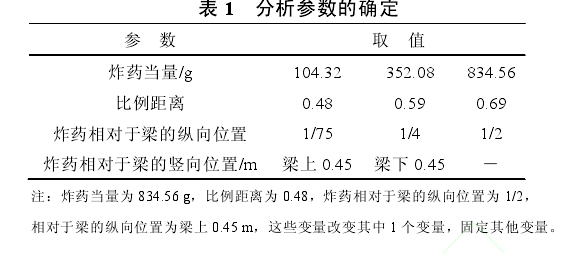
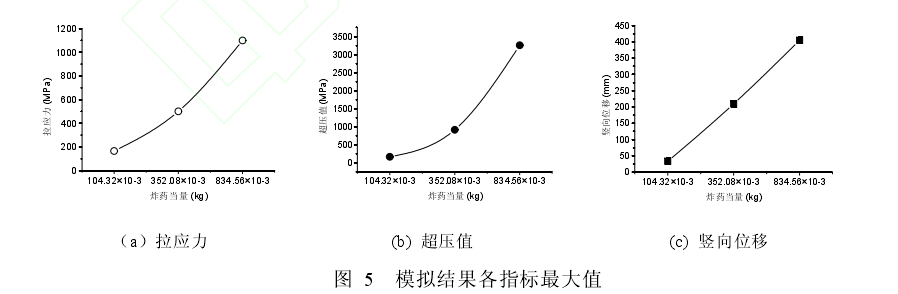
图4分别给出了3种不同炸药当量下,比例距离为0.48、炸药安放于梁体1/2跨径处及梁上0.45 m时模型测点相应分析结果的时程曲线。图5则给出了不同分析参数下测试指标的最大值。
通过图4和图5可知,当比例距离取0.48,炸药在梁上1/2跨径处时,随着炸药当量的增大,T梁测点的拉应力、超压值以及竖向位移近似呈线性增大。炸药当量104.32 g增加到834.56 g时,拉应力增大了5倍多,超压值增大了19倍,竖向位移增大了11倍。
2.2比例距离
对于冲击波各参数的表达常使用比例距离这一指标,比例距离的通常表达形式[12]为
式中:R为爆点中心距测点的距离,m;W为等效炸药药量,kg.
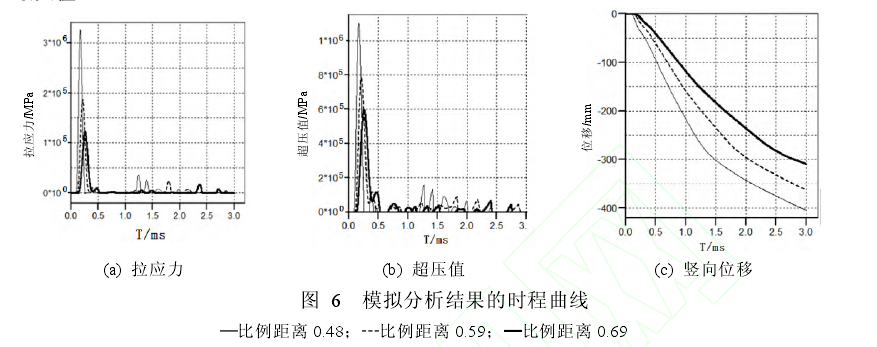
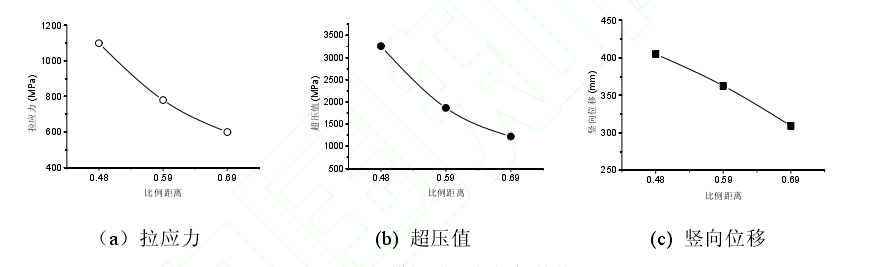
图6分别为3种不同比例距离,炸药当量取834.56 g,炸药放置位置为1/2跨径、梁上0.45 m时模型测试点分析结果相应的时程曲线。图7则给出了不同分析参数下测试指标的最大值。
通过图6和图7可知,当固定炸药当量为834.56 g及炸药位置在梁上1/2跨径2个参数时,以比例距离为单一改变参数进行研究,发现梁体损伤程度随着比例距离的增大而减小。比例距离由0.48增加到0.69时,拉应力减小45.5%,超压值减小62.4%,竖向位移减小23.7%.
2.3炸药和梁体相对纵向位置
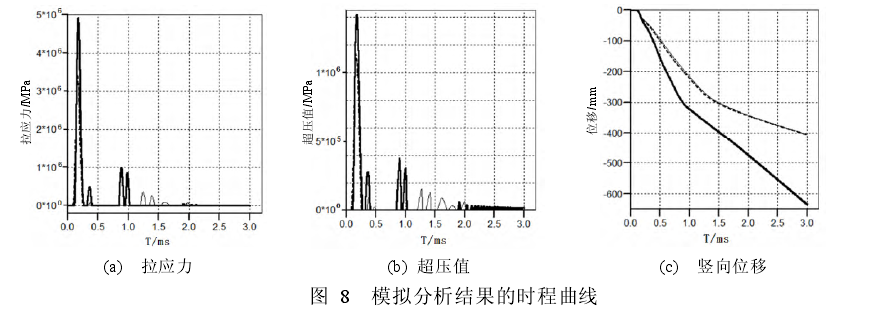
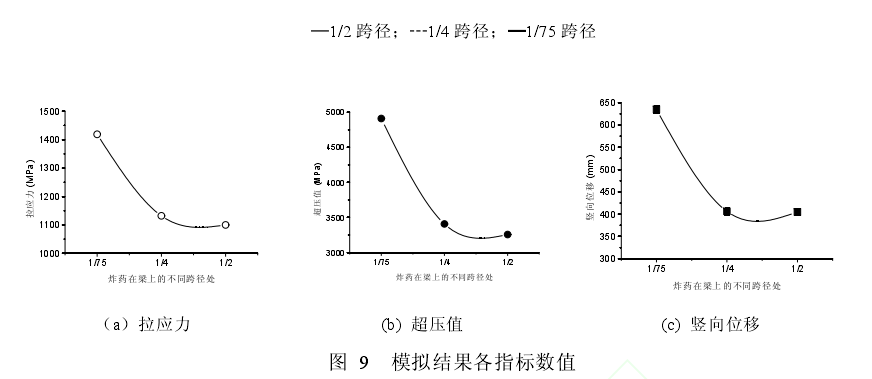
图8分别给出了炸药相对于梁体的不同纵向位置,比例距离为0.48,炸药当量为834.56g及置于梁上0.45 m时相应测点处模型分析结果的时程曲线。图9则给出了不同分析参数下测试指标的最大值。
由图8和图9容易看出,当炸药放置在梁上1/75跨径处时,梁体的损伤程度最严重。因此,可以认为炸药放置位置越接近梁端支座,梁的损伤也就越严重。一般梁体受冲击、爆炸等强荷载作用容易因弯曲变形产生破坏,如果爆炸产生的动荷载较大并且作用时间比较短,梁体在爆炸点处极易出现剪切破坏,并且爆炸点越接近梁端支座处产生的剪力也就越大,其损伤也就越严重。炸药在梁上由1/2跨径处变为1/75跨径时,拉应力增大了0.3倍,超压值增大了0.5倍,竖向位移增大了0.6倍。
2.4炸药在梁上1/2跨径处与梁下1/2跨径处对比
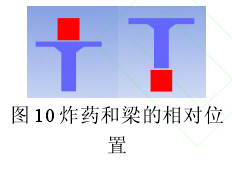
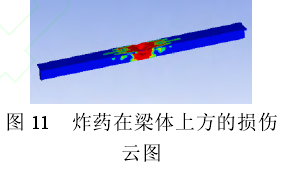
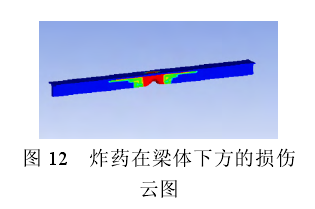
为考察炸药在梁横断面竖向相对位置的影响,本文将834.56 g的炸药分别放置在T梁跨中正上方和正下方约0.45 m处爆炸,如图10所示。图11和图12是炸药分别在梁体上方和下方3 m处爆炸发生时的梁体损伤。由图11、图12的损伤云图知,梁体受到爆炸荷载作用后主要发生了局部破坏,并且以破口形式存在。当爆炸物位于梁体上方时,跨中位置下挠严重,梁体跨中损伤破坏面积较大;当爆炸物位于梁体下方时,梁体跨中位置上拱,顶板有较小的损伤,损伤区域在底板跨中附近比较明显。炸药在梁上爆炸相比在梁下爆炸时迎爆面较薄,冲击波发生反射的次数较少,从而增加的能量较少,且因为翼板厚度小刚度小的特点,使其更加容易发生较大的破坏。所以迎爆面比较薄时,梁体损伤更加严重。由此可知,炸药放在梁上方比放在梁下方对梁的损伤严重。
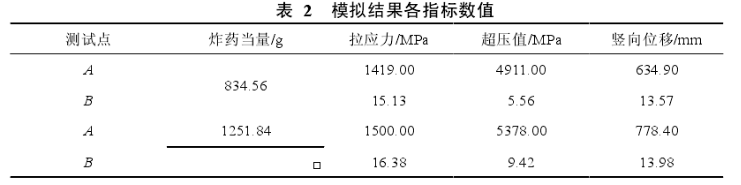
2.5梁体破坏的分析为确定第一强度准则、超压准则和最大挠度理论等3个评价指标的有效性,本文在炸药位置投影到梁底部的混凝土表面设定了测试点B.模型分析时将炸药安放在相对梁上1/75跨径处,比例距离0.48,炸药当量选为834.56 g,炸药放于梁体上部0.45 m,研究分析测点A、B处的拉应力、超压值及竖向位移等数值的变化情况,具体数值如表2所示。
根据第一强度准则,可以知道C35级混凝土的抗拉强度标准取2.20 MPa,40Cr Ni2Mo高强度钢的抗拉强度取980 MPa;根据超压准则,通过国防工程设计规范中规定的计算方法计算可以得出比例距离取为0.48时的超压临界值7.68 MPa;根据最大挠度理论,30 m跨径的梁的最大挠度为50 mm;当T梁的爆炸响应超过上述数值时,可认为梁体已经彻底破坏。由表2可知,当炸药当量达到1251.84 g时,无论是梁顶部测试点A还是底部测试点B处的超压值均已超过了超压临界值,使梁体彻底破坏。
3结束语
本文对桥梁工程中常用的T梁进行了数值模拟分析,结果表明:利用超压准则确定爆炸荷载作用下的梁体是否破坏可得到偏安全的计算结果;随着炸药使用当量的增大、安放比例距离的减小,钢筋混凝土梁体损伤程度将变大;炸药放在梁体上方产生的损伤比放在梁下方严重;炸药放置位置越靠近梁体端部,钢筋混凝土梁越容易发生剪切损伤。
参考文献(References):
[1] Rogers G L.Dynamics of framed structures[M].New York:Wiley,1959.
[2] Baker W E. Explosions in air[M]. Austin: University of Texas Press, 1973.
[3] Baker W E, Cox P A, Kulesz J J, et al. Explosion hazards and evaluation[M]. Amsterdam:Elsevier, 1983.
[4] Krauthammer T, Otani R K. Mesh, gravity and load effects on finite element simulations of blast loadedreinforced concrete structures[J].Computers & Structures, 1997, 63(6): 1113-1120.
[5] Krauthammer T, Assadi-Lamouki A, Shanaa H M.Analysis of impulsively loaded reinforced concretestructural elements-I: Theory[J].Computers & Structures, 1993, 48(5): 851-860.
[6] Krauthammer T, Assadi-Lamouki A, Shanaa H M.Analysis of impulsively loaded reinforced concretestructural elements-II:Implementation[J].Computers & Structures, 1993, 48(5): 861-871.
[7]方秦,吴平安。爆炸荷载作用下影响RC梁破坏形态的主要因素分析[J].计算力学学报, 2003, 20(1): 39-42.FANG Qin, WU Ping-an.The main factors damaging morphology under explosive load RC beam analysis[J].Chinese Journal of Computational Mechanics, 2003, 20(1): 39-42.
[8]柳锦春,方秦,龚自明,等。爆炸荷载作用下钢筋混凝土梁的动力响应及破坏形态分析[J].爆炸与冲击, 2003,23(1): 25-30.LIU Jin-chun,FANG Qin,GONG Zi-ming,et al.Response and failure modes of the power of reinforcedconcrete beam under explosive load[J]. Explosion and Shock Waves, 2003, 23(1): 25-30.
[9]张媛媛,郭东,令狐可,等。动载作用下钢筋混凝土梁非线性有限元分析[J].四川建筑科学研究, 2003, 29(4):19-20.ZHANG Yuan-yuan,GUO Dong, LINGHU Ke, et al. Dynamic load beams under the action of nonlinear finiteelement analysis of reinforced concrete[J].Building Science Research of Sichuan, 2003, 29(4): 19-20.
[10]焦延平,郭东,张虹,等。爆炸荷载作用下钢筋混凝土梁非线性有限元分析[J].振动与冲击,2003, 22(3):65-67.JIAO Yan-ping, GUO Dong, ZHANG Hong,et al.The explosion load nonlinear finite element analysis ofreinforced concrete beams[J].Journal of Vibration and Shock, 2003, 22(3): 65-67.
[11]张秀华,段忠东,张春巍。爆炸荷载作用下钢筋混凝土梁的动力响应和破坏过程分析[J].东北林业大学学报,2009,37(4):50-53.ZHANG Xiu-hua, DUAN Zhong-dong,ZHANG Chun-wei.Analysis of dynamic response and failure processof reinforced concrete beams under blast loading[J].Journal of Northeast Forestry University, 2009, 37 (4):50-53.
[12]吴宗之,高进东,魏利军。危险评价方法及其应用[M].北京:冶金工业出版社,2001.WU Zong-zhi,GAO Jin-dong,WEI Li-jun.Risk assessment method and its application[M].Beijing:Metallurgical Industry Press, 2001.
[13] 张国伟。终点效应及其应用技术[M].北京:国防工业出版社, 2006.ZHANG Guo-wei.The end effect and application technology[M].Beijing:National Defence Industry Press,2006.
[14] JTG D 62-2004,公路钢筋混凝土及预应力混凝土桥涵设计规范[S].JTG D 62-2004,Code for design of highway reinforced concrete and prestressed concrete bridges andculverts[S].