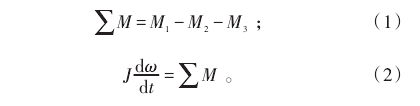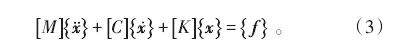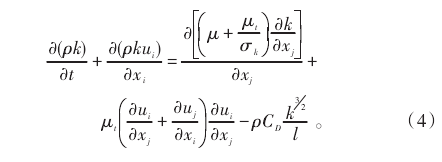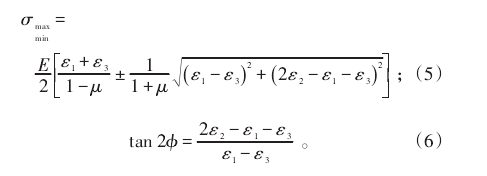摘 要
在对流固耦合仿真计算方法分析的基础上,建立起水下航行体舵板张开过程的仿真计算模型,采用该模型对舵板张开过程的角速度、载荷以及响应等变化规律进行了研究。在水下航行体发射试验中,对舵板张开角度、舵板应变等参数进行了测试,对测试获取的数据与仿真结果进行了对比分析,研究表明二者一致性较好,能够为水下航行体的水弹道分析和舵板的结构设计、材料选择等提供指导。
关键词:舵板;流固耦合;数值仿真;角速度
目 录
摘要
关键词
1基于流固耦合的仿真计算
1.1流固耦合计算模型分析
1.2仿真计算模型的建立
1.3仿真计算结果分析2舵板张开过程的试验数据分析
2舵板张开过程的试验数据分析
2.1测试方法
2.2试验数据分析
3结论
参考文献
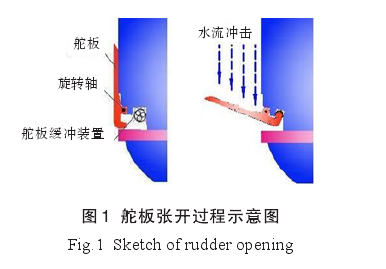
舵板是某水下航行体上的重要部件,当水下航行体以一定速度从发射管进入水中时,其尾部的舵板在水流冲击作用下及时、可靠张开,如图 1 所示,实现对水下航行体姿态的有效操控,同时承受张开瞬间的巨大冲击载荷。
在水下航行体从发射管发射入水时,管内燃气流产生的后效、航行体头部产生的空泡效应以及舵板周围流体形成的紊流等因素耦合作用在舵板结构周围,形成复杂的多相流场。因此,舵板的张开过程是在一个极其复杂的力学环境中完成的[1].
对舵板张开过程进行深入研究和分析,掌握其转动规律和张开到位时的冲击响应特性,对产品的设计具有重要意义。而要深入分析舵板张开特性,就必须采用仿真计算和试验相结合的方法,才能获得较好的研究效果。
1基于流固耦合的仿真计算
1.1流固耦合计算模型分析
舵板张开过程受到航行体运动速度、舵板表面压强以及航行体尾流场的影响;反之,舵板的转动又影响周围流场的变化,这二者相互作用、相互影响,因而这一过程属于典型的流固耦合问题。流固耦合的概念在 1933 年由 H.M.Westergaard 提出,但真正发展却是从 20 世纪 80 年代之后。在近 30 年中,流固耦合数值计算经历了解耦-弱耦合-强耦合的发展过程[2-4],相应建立流固耦合模型的方法也分为以下3种。
1)古典分析法。将内部耦合的非线性问题分解为2个独立的解耦问题分别求解。因此,从严格意义上讲,古典分析法还不是一种真正的流固耦合方法。
2)交错积分分析法。首先对流体作用下的结构响应进行积分,推至下一时刻,将结构边界位移和运动传递给流体系统,更新流体动态网格,然后进行流体积分计算新的压力场,再将流体压力转换成结构载荷,传递给结构重新进行计算,如此往复循环[5].
3)整体积分法。将流体和结构看作通过耦合界面连接的单一连续介质,用单一的算子描述整个计算场的控制方程。
以上 3 种方法中,整体积分法在 2 个场中的时间积分完全同步,不存在时间滞后和能量不守恒现象,是一种完全的强耦合方法,也是解决流固耦合问题最理想的方法。但在实际应用中,将流体和固体的控制方程完全结合起来尚存在一定难度,且同步求解的收敛性差,占用机时资源大,因而该方法目前只应用于一些简单问题的求解,尚未得到广泛应用。
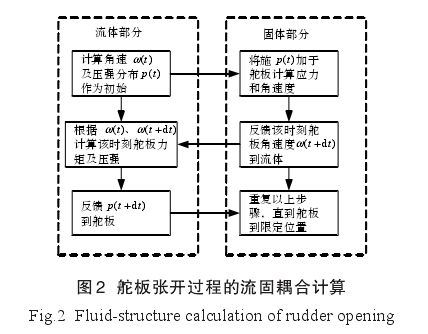
本文采用交错积分法建立舵板张开过程的仿真计算模型,其计算过程如图2所示。
1.2仿真计算模型的建立
1)控制方程。由于本文采用了交错积分方法开展仿真计算,因而舵板张开运动及动力学计算和流场计算分别采用相应的控制方程。舵板运动学方程为:
式(1)、(2)中:M1、M2、M3分别为流体的推动力矩、缓冲管的反作用力矩和销轴的摩擦力矩;J 为舵板转动惯量。舵板运动到位后的动力学方程为:
式(3)中:[M]、[C]、[K]分别是舵板的质量矩阵、阻尼矩阵和刚度矩阵;{x}为舵板运动的位移矩阵;{f}为作用在流体舵板上的压力载荷矩阵。
综合权衡计算对象特点以及计算效率,流场计算采用一方程模型对湍流流动现象进行模拟。一方程模型是在时均连续方程和雷诺方程组成的方程组的基础上,再建立一个湍动能 k 的输出方程,而湍动黏度 μt表示成 k 的函数,从而使得方程组封闭。湍动能k 的输运方程可写为[6-7]:
式(4)中:Ui、Uj为速度分量;μ 为流体动力粘度;σk、CD为经验常数;l为长度比尺。
2)几何模型的简化。水下航行体及舵板结构复杂,建模时需对舵板的局部区域做合理简化:去掉舵板上凹槽及初始分离机构,将航行体表面假设为平整表面,对舵板根部做适当切除,但应确保简化后的舵板转动轴心与实际转轴中心保持相同,且转动惯量发生的变化可以被忽略。
3)计算域模型的确定。计算域是包围水下航行体和舵板的大圆柱体(水域)。根据经验,当水域直径为水下航行体直径 20 倍时,可满足计算精度要求,不会因边界设置对流场计算产生影响。水域上表面为海水表面,即水域高度为水下航行体的发射水深。
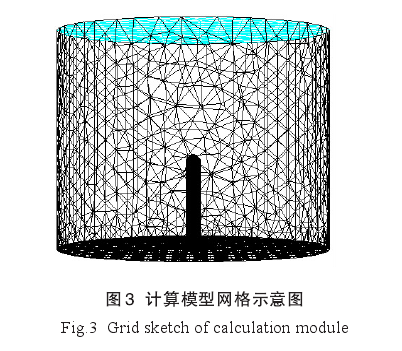
4)计算网格的划分。为保证计算准确性和收敛性,需合理进行网格划分。水下航行体附近网格较密,其中舵板与水下航行体之间的网格最为密集;远离水下航行体、流动变化小的部位网格较稀疏。因采用动网格技术,模型中的网格均为四面体网格[8-9].网格生成后,应用 Smoother 工具进行了优化,得到质量较高的计算网格,如图3所示,网格数量共43万。
5)初始条件的确定。计算中,将初始时刻确定为舵板初始张开瞬间。由于舵板模型简化时已去掉初始分离机构,使得舵板在0°时不存在驱动舵板转动的载荷,故采用初始时刻试算的方法,确定一个合理的初始位置以启动分析计算。以一个初始的角度进行流场迭代,当计算能够收敛即流场状态稳定时,将此初始角确定为计算初始时刻。经仿真试验,计算初始时刻确定为舵板张开夹角5°。
6)边界条件的设定。将位于水下航行体尾部的发射筒口设为压强入口边界条件,给定发射筒喷气的总压,随着航行体向上运动,喷气总压随之不断下降。计算域的上表面(自由表面)为压强出口条件,静压值为一个标准大气压。由于流体粘性的存在,固体表面设定无滑移边界条件,其余边界,如计算域的侧面和底面均是由假想表面与海水相交组成,设定为滑移边界条件[10-11].
1.3仿真计算结果分析
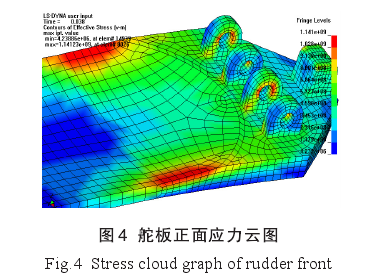
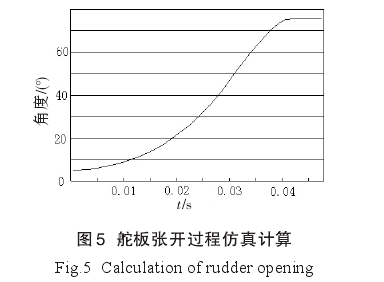
采用建立起的仿真计算模型,得到不同时刻舵板的流体载荷及其旋转驱动力矩,据此计算出舵板的角加速度和角速度,进而确定舵板的运动规律,同时计算出舵板上的应力分布,如图4、5所示。
在舵板张开到位瞬间,受到一个较大的冲击载荷。此时,在舵板正面两侧边缘、舵板耳座等部位出现较大的应力,见图4,最大应力达到1 141 MPa,最小应力为422 MPa.经分析,舵板两侧边缘、舵板耳座应力较大与实际工况是相符的,但因这些部位均处于边缘或夹角处,故计算误差可能造成计算值偏大。
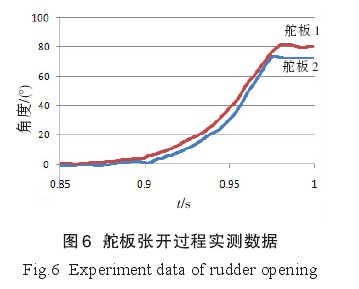
由图5可知,舵板张开到位时间约为43 ms,张开角度约为76°。在舵板张开过程中呈现明显的加速运动趋势,前20 ms舵板张开角度约为15°,后20 ms舵板张开角度约为56°,与实际物理规律一致:即舵板张开初期,作用在舵板上的转动力矩较小,随着舵板张开角度的增大,作用在舵板上的水动力开始增加,相应的转动力矩也逐渐变大,使得舵板作加速运动。舵板张开过程实测数据见图6.
2舵板张开过程的试验数据分析
2.1测试方法
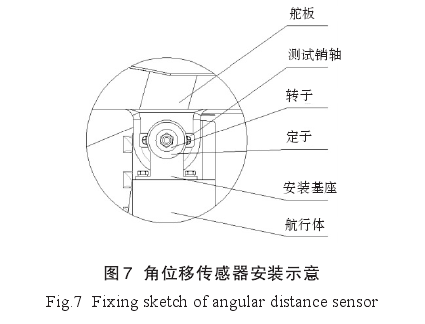
舵板转动测试采用角位移传感器。角位移传感器的实质是一个旋转变压器,其转子固定在测试销轴上,该测试销轴和舵板运动规律保证一致;在航行体表面安装固定基座,角位传感器的定子安装在此固定基座上,如图7所示。当舵板由于水流冲击张开时,舵板测试销轴的转动就会带动角位移传感器转子转动,由于角位移传感器定子部分被固定,因而在定子和转子之间会产生磁力线切割,角位移传感器产生电压信号,经数据转换器变换和处理后,获得舵板转动角度-时间曲线。
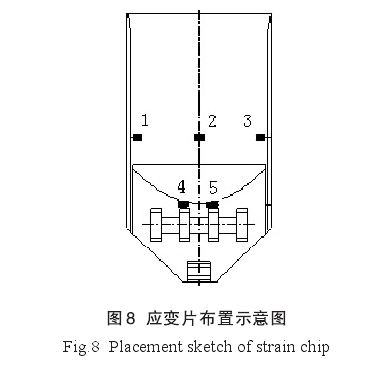
依据仿真计算结果,在舵板正面两侧边缘、中间以及舵板耳座布置了应变片。其中,舵板耳座位置为三向应变片,其他位置为单向应变片,单向应变片方向与舵板轴向一致[12-13].应变片布置如图8所示。
2.2试验数据分析
某发次试验中,2个角位移传感器获取的数据如图6所示。2个传感器测得的舵板最大转角分别为81°和74°,与仿真计算结果相符较好。舵板张开时间分别为83 ms和77 ms,这一数据大于仿真计算的43 ms.经分析,造成这一现象的原因主要有2点:一是在仿真计算中预置了5°的初始角度,造成舵板实际张开时间大于计算值,根据测试数据或仿真计算结果,舵板初始5°转动中消耗的时间大约为20 ms左右;二是仿真计算得出的转动力矩大于实际值,从舵板的实际角位移曲线也可以看出,计算得到的舵板角速度要大于实际舵板运行角速度。
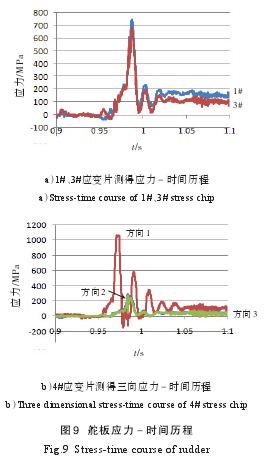
试验中,1#和 3#应变片、4#三向应变片测试获取的曲线如图9所示。
1#、3#应变片测得的最大应力分别为732 MPa和689 MPa,二者在整个时间历程中吻合性较好,这说明测试数据准确可信。测试值小于计算值充分验证了1.3 节中的分析:在计算中,舵板建模时未对其边缘进行倒角处理,导致计算中出现明显的应力集中和相应的计算误差;在实际工况中,舵板边缘存在一个较大倒角;此外,实际测试中应变片与舵板边缘有10 mm距离,也使得测试中舵板边缘的应力明显小于计算值。
从4#三向应变片可以看出,在舵板耳座表面位置存在两向应力,但在一个方向主应力明显大于另外一个方向。
按式(1)、(2)可分别进行计算主应力大小和方向:
式(5)、(6)中:ε1、ε2、ε3为0°、45°、90°方向上测得的应变;E 为材料弹性模量(MPa);μ 为波松比。
计算得耳座最大主应力约为1100 MPa,超过舵板材料的屈服强度,且接近强度极限。经进一步分析可知,在数据处理中按应力-应变为线性关系进行处理,即将应变片测试值直接乘弹性模量得到该点应力。这一处理方法在结构弹性变形范围内是适用的,但若结构发生塑性变形,这样的数据处理方法就会大大放大应力值[14- 15].为取得真实的应力值,重新测试舵板材料的应力-应变曲线,获取该材料破断之前完整的应力-应变关系曲线,根据该曲线得出测试应变所对应的实际应力。经再次处理后,4#位置最大应力为864 MPa,略高于屈服强度。这说明该舵板耳座与本体连接处会产生一定塑性变形,但不会影响舵板安全工作。舵板张开到位后正常工作角度时,舵板上的应力约为100~200 MPa,远小于舵板屈服强度。
3结论
通过仿真计算和试验结果,可得出以下结论。
1)舵板到位后张开角度约为80°左右,完全能够满足对水弹道的姿态控制要求,舵板张开呈加速运动趋势,张开到位时间大约在70~80 ms之间,和水下航行体在水中的整个运动时间相比是一个小量,因而舵板张开过程不会对水下航行体的水弹道控制造成影响。
2)舵板张开位移-时间历程的仿真计算和实验实测数据吻合较好。
3)实验结果表明:舵板的张开过程工作在一个复杂的紊流环境中。不同发次中,舵板相同部位的应力存在一定离散。
4)仿真与实验测量均表明:舵板张开到位正常工作角度时,应力不足200 MPa,能够确保其安全可靠工作;但当舵板和缓冲装置接触时,在舵板上产生一个最大值约为860 MPa的应力冲击,会造成舵板产生一定塑性变形,这就要求在舵板材料选择时,应重点考虑材料的冲击韧性和塑性指标。
参考文献:
[1] 罗金玲,何海波。 潜射导弹的空化特性研究[J]. 战术导弹技术,2004(3):14-17.LUO JINLING,HE HAIBO. Research on cavitation forunder- water launching missile[J]. Tactical Missile Tech-nology,2004(3):14-17.(in Chinese)
[2] 张阿漫,戴绍仕。 流固耦合动力学[M]. 北京:国防工业出版社,2011:2-3.ZHANG AMAN,DAI SHAOSHI. Fluid solid interactiondynamics[M]. Beijing:National Defense Industry Press,2011:2-3.(in Chinese)
[3] 任弘,李范春,杜玲。 流固耦合作用对螺旋桨强度影响的数值计算[J]. 武汉理工大学学报,2015,39(1):43-52.REN HONG,LI FANCHUN,DU LING. Numerical calcu-lation for the effect of fsi on marine propeller strength[J].Journal of Wuhan University of Technology,2015,39(1):43-52.(in Chinese)
[4] YOUNG Y L. Fluid-structure interaction analysis of flexi-ble composite propellers[J]. Journal of Fluids and Struc-tures,2008,24:799-818.
[5] 宋学官,蔡林,张华。 ANSYS 流固耦合分析与工程实例[M]. 北京:中国水利水电出版社,2012:5-9.SONG XUEGUAN,CAI LIN,ZHANG HUA. ANSYSfluid solid interaction analysis and engineering examples[M]. Beijing:China Water Power Press,2012:5- 9. (inChinese)
[6] 周俊杰,徐国权,张华俊。 FLUENT 工程技术与实例[M].北京:中国水利水电出版社,2013:8-13.ZHOU JUNJIE,XU GUOQUAN,ZHANG HUAJUN.FLUENT engineering technology and case[M]. Beijing:China Water Power Press,2013:8-13.(in Chinese)
[7] 张磊,郎进花,王松岭。 流固耦合问题数值模拟算法研究进展[J]. 热力发电,2015,44(1):1-7.ZHANG LEI,LANG JINHUA,WANG SONGLING.Recnt development of numerical simulation methods forfluid-structure interaction[J]. Thermal Power Generation,2015,44(1):1-7.(in Chinese)
[8] 都军民。 潜基导弹发射动力系统推力能控制技术研究[D]. 大连:大连理工大学,2008:72-73.DU JUNMIN. Available energy control in submarine-based missile launch power system[D]. Dalian:DalianUniversity of Technology,2008:72-73.(in Chinese)
[9] 刘维伟,张定华,王军伟。 叶片造型万个扭曲的校正方法研究[J]. 机床与液压,2004(1):65-67.LIU WEIWEI,ZHANG DINGHUA,WANG JUNWEI.Research on rectification technology of parametric griddistortion in blades modeling process[J]. Machine Tooland Hydraulics,2004(1):65-67.(in Chinese)
[10] DU JUNMIN,HU LIZHONG,KANG NING,et al. Nu-merical simulation of the add mass and drag of an acceler-ated motion ball[C]//2014 International Conference onMechanics and Materials Engineering. Xi'an,2014:104-109.
[11] 李秋实,徐飞,李志平。 一种包含运动边界的高精度流场数值计算方法[J]. 航空学报,2014,35(7):1815-1824.LI QIUSHI,XU FEI,LI ZHIPING. A numerical methodfor simulation flow involving moving boundaries withhigh order accuracy[J]. Acta Aeronautica et AstronauticaSinica,2014,35(7):1815-1824.(in Chinese)
[12] 孙晓丹,侯钢领,王月敏,等。 基于灵敏度的平板结构多类型传感情优化布置[J]. 工程力学,2015,32(4):77-84.SUN XIAODAN,HOU GANGLING,WANG YUEMIN,et al. Optimal placement of multi- type sensor based onsensitivity for plate structure[J]. Engineering Mechanics,2015,32(4):77-84.(in Chinese)
[13] TANG Z Z,LIANG J. Three dimensional digital imagecorrelation system for deformation measurement in exper-imental mechanics[J]. Optical Engineering,2010,49:013601-1-9.
[14] 张川,郭楠。 超大变形应变测量方法的研究[J]. 中国测试,2014,40(S1):90-93.ZHANG CHUAN,GUO NAN. Research on large defor-mation strain measurement method[J]. China Measure-ment & Test,2014,40(S1):90-93.(in Chinese)
[15] 郭芳,杨录,张艳花。 应用超声波技术对材料应力特征的提取与分析[J]. 声学技术,2008,27(2):217-220.GUO FANG,YANG LU,ZHANG YANHUA. Measure-ment and analysis of material stress with ultrasonic tech-nology[J]. Technical Acoustics,2008,27(2):217- 220.(in Chinese)